Program realizacji całorocznego konkursu matematyczno - fizycznego dla gimnazjalistów

I. Wstęp
Uczniom gimnazjum wciąż brakuje konkursów szkolnych. Te zewnętrzne dla wielu okazują się za trudne i mało dostępne. Zrodził się więc pomysł organizacji konkursu o zasięgu szkolnym, ale takiego, by mógł w nim wziąć udział uczeń każdej klasy, zarówno pierwszej, jak też trzeciej; ten osiągający dobre wyniki, jak i ten słabszy. Każdy musi znaleźć coś dla siebie. Tak powstał całoroczny konkurs matematyczno - fizyczny „Rozmaitości matematyczno - fizyczne”. Konkurs będzie trwał od września do maja w roku szkolnym 2003/2004.

II. Cele konkursu

• popularyzowanie wiedzy matematycznej i fizycznej;
• realizacja niektórych zagadnień ze ścieżek międzyprzedmiotowych;
• wzbudzanie zainteresowań matematycznych i fizycznych wśród gimnazjalistów;
• identyfikacja i promocja młodzieży uzdolnionej w kierunku matematyczno - fizycznym;
• przygotowanie do testów gimnazjalnych;
• samoocena własnych możliwości i zainteresowań;
• wdrażanie do samodzielności w poszukiwaniu i poszerzaniu wiedzy;
• doskonalenie umiejętności dostrzegania różnorodnych zjawisk i problemów w przyrodzie i formułowania wniosków;
• doskonalenie umiejętności opracowywania wyników i przedstawiania ich w czytelnej formie.

III. Zagadnienia objęte konkursem
Podstawa programowa w zakresie matematyki i fizyki w gimnazjum oraz niektóre zagadnienia poza programowe, możliwe do samodzielnego opracowania przez uczniów, ciekawostki i zadania logiczne.

IV. Informacja o konkursie
Już na początku roku szkolnego na szkolnej tablicy ogłoszeń pojawiła się następująca informacja:

V. Etapy konkursu
W załączeniu, w takiej formie, w jakiej pojawiały się na tablicy ogłoszeń, wraz z propozycją przyznawania punktów.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap I
Problem 1. Dlaczego butelka z napojem wyjęta z lodówki pokrywa się kropelkami wody? (1 pkt)
Problem 2. W fabryce słodyczy stoi sześcian z czekolady o krawędzi 2 dm. Czy tej czekolady wystarczy do sporządzenia 150 tabliczek o wymiarach 15 cm x 5 mm x 8 cm ? Przedstaw obliczenia. (2 pkt)
Problem 3. Ile razy wskazówki zegara w ciągu doby tworzą kąt prosty ? Uzasadnij wynik. (2 pkt)
Problem 4. Co w próżni spadnie szybciej: piórko czy kamyk? Dlaczego? (1pkt)
Problem 5. Znajdź informacje o systemie dwójkowym zapisywania liczb i przedstaw tym sposobem liczby : 3, 10, 67, 235. (4 pkt)
Odpowiedzi będą przyjmowane do 19 września 2003 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap II
Problem 1. Dlaczego na wysokiej górze trudniej jest ugotować mięso czy warzywa? (1 pkt)
Problem 2. Liczbę 75 rozłóż na takie dwa składniki, aby ich różnica była trzykrotnie mniejsza od większego z nich. (2 pkt)
Problem 3. Co to są hologramy i jak je można stosować?(2 pkt)
Problem 4. Karol stoi przed wysoką ścianą skalną. Dwie sekundy po klaśnięciu w dłonie słychać echo. W jakiej odległości od Karola znajduje się skała?
Wskazówka: znajdź prędkość dźwięku w powietrzu. (1 pkt)
Problem 5. Trzech sponsorów ufundowało wspólnie nagrodę pieniężną. Pierwszy dał czwartą część sumy i 30 tys. zł, drugi dał trzecią część sumy i 20 tys. zł, a trzeci dał o 16 2/3 % mniej niż pierwszy. Jaka była wysokość nagrody? (3 pkt)
Odpowiedzi będą przyjmowane do 20 października 2003 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap III
Problem 1. W środku basenu jest fontanna. Woda wytryska z niej 16 rurkami o średnicy 0,5 cm każda. Basen jest opróżniany za pomocą otworu o średnicy 2 cm. Dozorca otworzył dopływ wody do fontanny, ale zapomniał zamknąć otwór odpływowy. Po jakim czasie woda wypełni basen? (2 pkt)
Problem 2. Co to jest konchoida? Wykonaj rysunek. (2 pkt)
Problem 3. Ile różnych trójkątów można zbudować z odcinków o długościach : 29 cm, 14 cm, 12 cm, 6 cm, 19 cm. Odpowiedź uzasadnij. (2 pkt)
Problem 4. Co to jest burza magnetyczna i jakie może wywołać skutki? (1 pkt)
Problem 5. Pomiędzy dwa wózki o masach m₁=2 kg i m₂=6 kg wstawiono naprężoną sprężynę. Po zwolnieniu sprężyny wózki wskutek oddziaływania sprężystego rozjechały się. Pierwszy uzyskał prędkość o wartości v₁=12 m/s, oblicz prędkość drugiego wózka.
Wskazówka: skorzystaj z zasady zachowania pędu. (3 pkt)
Odpowiedzi będą przyjmowane do 10 listopada 2003 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap IV
Problem 1. W małym pudełku mieści się 48 zapałek. Ile takich samych zapałek zmieści się do pudełka podobnego do danego w skali 3:1? (2 pkt)
Problem 2. Dlaczego taśmy magnetofonowe i magnetowidowe należy przechowywać z dala od źródła pola magnetycznego? (1 pkt)
Problem 3. Co oznaczają w matematyce (lub w jej dziale - statystyce) pojęcia: moda i mediana? Podaj przykłady. (3 pkt)
Problem 4. Masa Kasi wynosi 40 kg. Jej mięśnie wykorzystują 20% energii otrzymanej z pożywienia. Jak wysoko może wejść Kasia dzięki energii 8000 dżuli pochodzącej z jednego cukierka? Wykonaj obliczenia. (3 pkt)
Problem 5. Półtora kota zjada półtora myszy w ciągu półtora dnia. Ile myszy zje 7 kotów w ciągu tygodnia? (1 pkt)
Odpowiedzi będą przyjmowane do 28 listopada 2003 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap V
Problem 1. Co to jest złoty podział odcinka? Podaj przykład konstrukcji. (1 pkt)
Problem 2. Czy silny gimnazjalista jest w stanie podnieść na wysokość 1,2 m pojemnik o pojemności 5 litrów wypełniony rtęcią? (2 pkt)
Problem 3. W pewnej klasie 5 osób ma oceny bardzo dobre z matematyki, 7 osób oceny dobre, 9 osób oceny dopuszczające i 1 osoba ma ocenę niedostateczną. Ile osób w tej klasie ma oceny dostateczne, jeżeli średnia ocen z matematyki wynosi 3,2? (3 pkt)
Problem 4. Z ośmiu kostek do gry sklejono sześcian. Suma oczek na wszystkich widocznych ściankach jest o 8 mniejsza niż na ściankach niewidocznych. Ile oczek jest na ściankach niewidocznych? (2 pkt)
Problem 5. Żelazny pręt o przekroju 1 cm² ma masę 3,16 kg. Jaką ma długość ten pręt? (2 pkt)
Odpowiedzi będą przyjmowane do 19 grudnia 2003 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap VI
Problem 1. Znajdź wzór Herona z Aleksandrii na obliczanie pola trójkąta i na jego podstawie oblicz pole trójkąta o bokach 12 cm, 11 cm i 10 cm. (2 pkt)
Problem 2. Pasażer jadący pociągiem ze średnią prędkością 60 km/h obserwuje przez okno swojego wagonu mijający go pociąg jadący z prędkością średnią 40 km/h. Mijanie trwało 6 s. Jaką długość miał pociąg widziany z okna? (2 pkt)
Problem 3. Na podstawie dialogu ustal wiek wujka:
- Wujku, ile masz lat?
- Dwa razy tyle, co kuzynka Hania.
- A ile lat ma kuzynka Hania?
- Trzy razy mniej od cioci Ewy.
- A ile lat ma ciocia Ewa?
- Ciocia Ewa ma o 20 lat więcej od Zosi.
- A ile lat ma Zosia?
- Zosia ma 5 razy tyle, co Ania.
- A ile lat ma Ania?
- Oj, przestań nudzić, za rok będzie miała 6 lat.
- ??? (3 pkt)
Problem 4. Na planie miasta w skali 1:20 000 ogród zoologiczny jest prostokątem o wymiarach 4 cm x 5 cm. Jaka powierzchnię zajmuje ZOO w rzeczywistości? (2 pkt)
Problem 5. Ola pokonała w górach różnicę wzniesień 50 m, a Kasia – 100 m w tym samym czasie. Moc której dziewczynki jest większa, jeżeli masa Oli to 60 kg a Kasi 30 kg? (1 pkt)
Odpowiedzi będą przyjmowane do do 30 stycznia 2004 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap VII
Problem 1. Odszukaj w jaki sposób potęgujemy liczby, jeżeli wykładnik potęgi jest ułamkiem? Na tej podstawie wykonaj potęgowanie:

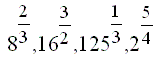
(4 pkt)
Problem 2. Dwaj chłopcy o masach 40 kg i 60 kg stoją naprzeciw siebie na wrotkach. W pewnej chwili lżejszy odpycha cięższego z siłą 20 N. Oblicz jakie przyspieszenie uzyskają chłopcy? Z której zasady dynamiki skorzystasz? (2 pkt)
Problem 3. Z nadmuchanego balonu wypuść powietrze przez mały otwór (np. zrobiony szpilką) na dłoń lub czuły termometr. Dlaczego powietrze wypuszczane z balonu jest zimniejsze niż temperatura otoczenia? (1 pkt)
Problem 4. O ile zwiększy się objętość sześcianu jeżeli krawędź zwiększymy o 10% ? (2 pkt)
Problem 5. Ile liczb trzycyfrowych parzystych można utworzyć z cyfr 1, 2, 3, 4? (1 pkt)
Odpowiedzi będą przyjmowane do 5 marca 2004 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap VIII
Problem 1. Dlaczego ostry nóż tnie lepiej, niż nóż tępy? (1 pkt)
Problem 2. Co to jest regelacja? Podczas jakiego doświadczenia można by było ją zaobserwować? (2 pkt)
Problem 3. Dlaczego kolumna żołnierzy idąc przez długi most zmienia krok na nierówny? (1 pkt)
Problem 4. Przyrost pewnej rośliny jest stały i wynosi tygodniowo 1,5 cm. Obserwację tej rośliny rozpoczęto w dniu, w którym roślina miała 4,5 cm.

1. Sporządź tabelkę i wykres zmian wysokości tej rośliny w kolejnych czterech tygodniach obserwacji.
2. Jaką wysokość miała roślina po 10 dniach?
3. Ile tygodni przed obserwacją roślina wykiełkowała?

(4 pkt)
Problem 5. Znajdź wartość a wiedząc, że liczba 0,125 jest rozwiązaniem równania:

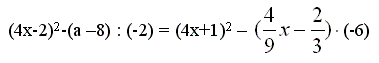
(2 pkt)
Odpowiedzi będą przyjmowane do 25 marca 2004 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap IX
Problem 1. Cegłę o wymiarach 20 cm x 15 cm x 10 cm wrzucono do wody. Jaka siła wyporu działa na cegłę? (2 pkt)
Problem 2. Co to jest kwaterka?. Ile cm³ zawierają trzy kwaterki? (1 pkt)
Problem 3. Oblicz objętość ostrosłupa prawidłowego czworokątnego, którego pole powierzchni bocznej wynosi 544 cm², a pole powierzchni całkowitej 0,08 m² (4 pkt)
Problem 4. Telewizor 28 calowy to taki, którego ekran jest prostokątem o przekątnej 70 cm (1 cal to około 2,5 cm). Oblicz bok kwadratowego ekranu telewizora 25 calowego. (2 pkt)
Problem 5. Jaką wielkość fizyczną określa się w bekerelach? (1 pkt)
Odpowiedzi będą przyjmowane do 28 kwietnia 2004 r.

Konkurs „Rozmaitości matematyczno - fizyczne” - etap X - finałowy
Problem 1. Ile wody należy dolać do 1 litra octu 10%, aby otrzymać roztwór 5%? (3 pkt)
Problem 2. Czekolada kosztuje 2,30 zł, a herbatniki są 2 razy tańsze od czekolady. Ile zapłacono za 3 czekolady i dwie paczki herbatników?(1 pkt)
Problem 3. Średnica obranej ze skórki pomarańczy wynosi 8 cm. Wyciśnięty z niej sok stanowi 40% jej objętości . Ile trzeba obrać pomarańczy, aby otrzymany z nich sok napełnił naczynie o objętości 1 litr? (3 pkt)
Problem 4. Przez przewodnik płynie prąd o natężeniu 2A. Jaki ładunek przepłynie przez poprzeczny przekrój przewodnika w ciągu 1 minuty? (2 pkt)
Problem 5. W jaki sposób można wyznaczyć kształt linii pola magnetycznego magnesu sztabkowego? (1 pkt)

VI. Podsumowanie
Zgodnie z zapowiedzią konkurs trwał cały rok szkolny, brało w nim udział ok. 25 gimnazjalistów, niektórym brakło wytrwałości i odpadali po kolejnych etapach, niektórzy dołączali w trakcie. Uczniowie w większości udzielali poprawnych i starannych odpowiedzi. Była to także powtórka przed egzaminem gimnazjalnym Do końca wytrwało 13 osób z klas II-III. Wszyscy uczestnicy otrzymali dyplomy udziału, a najlepsza szóstka wartościowe nagrody książkowe ufundowane przez Radę Rodziców. Ponadto uczniowie zostali nagrodzeni odpowiednimi do swoich wyników ocenami z matematyki i fizyki.

Konkurs okazał się więc próba dla najwytrwalszych i cierpliwych, wymagał systematycznej pracy poza normalnymi zajęciami. Uważam, że tego rodzaju konkursy będą się cieszyły popularnością, należałoby tylko skrócić czas ich trwania, zachęcimy wtedy większą liczbę uczestników.

Z opinii uczniów wiem, że konkurs został odebrany pozytywnie i padają pytania czy będzie się organizowany w kolejnych latach. Zachęcam innych nauczycieli do organizowania podobnych form aktywności uczniów.

Opracowała i wdrożyła w roku szkolnym 2003/2004:
mgr Gabriela Małek - Miedzińska
Zespół Szkół Gimnazjalnych i Ponadgimnazjalnych we Włosieniu